Objectives

One of my favorite problems is calculating pi based on probability. This blog post will show you how to do that with python, c#, and ocaml. Basic knowledge of computer programming, in any one of those languages, will definitely be an asset. This post can also show you how to translate from a language that you know to a new one.

PI

pi is an irrational constant that is the ratio of a circle’s circumference to its diameter

It is also used to calculate a circle’s area.

If we overlay a circle on a square as shown below we can compare the differences in the area of the two.

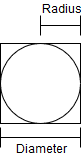
So if we were to randomly choose any location on the square what would be the probability that the location would also be inside the circle. The probability is just the ratio of areas.

So the chance that we hit the inside of the circle is $\frac{\pi}{4}$.

Making it computationally easier.

Let’s just look at $\frac{1}{4}$ of the drawing. This will make a bit more sense later on.

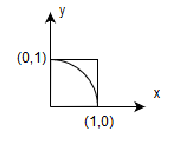
In this diagram, the radius of the circle is 1. The probability of being in the $\frac{1}{4}$ circle when choosing a random position inside the smaller square is still the same probability as in eq 5. This is because we have divided the area of both by 4. This diagram also shows an x and y-axis with an origin at the centre of the original circle.

Ok. So if we can generate two random numbers between 0 and 1, we can use the first random number to represent an x coordinate and the second number to represent a y coordinate. We just need some equation to govern whether the randomly chosen x and y coordinate are inside the $\frac{1}{4}$ circle.

We can use the Pythagorean theorem to help us. We know that the radius of the circle is always 1. So…

Calculating with Python

Ok, let’s start with python.

We will be using a few premade python libraries. So the first step is to import these libraries in.

import math
import random

this allows us to use math functions like square root and power as well as a function to generate random numbers. We can perform those operations like this.

sqrt_2 = math.sqrt(2)    # return square root of 2 inside the variable sqrt_2
nine = math.pow(3,2)   # returns 9 inside the variable nine
random_num = random.random() # returns a random number between 0 and 1 inside the variable random_num

It is a little tedious to keep writing the words math and random, so instead, we can import all functions of these two libraries and call the functions directly.

from math import *
from random import *

After importing the libraries we need to generate a variable to hold the total number of iterations we will perform and the number of times those iterations succeed in being inside the $\frac{1}{4}$ circle.

total_iterations = 1000000
count_inside_quarter_circle = 0

Next, we can start looping through all of the iterations. The easiest way to make a for loop in python is using the range keyword. This block of code will run multiple times while changing the value of i from 0 to total_iterations.

for i in range(total_iterations):
  ...

With Python, we have to be careful about our indentations and note that there is a colon after a function, loop, or if statement.

for i in range(total_iterations):
  x = random()
  y = random()
  if sqrt(pow(x,2) + pow(y,2)) < 1:
    count_inside_quarter_circle = count_inside_quarter_circle + 1

Finally, we can then print out our answer for pi.

print(4 * count_inside_quarter_circle / total_iterations)

You can test this online at https://repl.it/ or https://www.python.org/shell/.

The full file should look like this.

Calculating with C#

Ok, so this starts off very similar to python. Start off with our imports. In c# we use the using keyword.

using System;
using System.Math;

Next, we construct the main body of our program. We need to make a class and the main function. This is how the compiler knows where the program starts. You need to do something similar in python when you have larger projects, but python interprets everything at runtime line by line, so smaller projects are fine.

class MainClass {
  public static void Main (string[] args) {
    //Program Code
  }
}

In c# we need to define variables and the type of data associated with them. We will be using integer variables and doubles. Doubles are numbers that can hold decimal values.

int total_iterations = 100000000;
int count_inside_quarter_circle = 0;

We can generate random numbers using the Random class.

Random r = new Random(); //initialize a new object of the class random
double x = r.NextDouble(); //return random number between 0 and 1 stored in variable x
double y = r.NextDouble(); //return random number between 0 and 1 stored in variable y

With for-loops, we may pass three different operations. The first may be a variable initializer, the second is a condition that will stop the loop, and finally, we have an operation that will be done at the end of each loop. Any or all of these may be blank.

int k = 0;
for (int i = 0; i < total_iterations; i++){

  if (LOGIC_STATEMENT)
    k++; //only do the very next line because there are no brackets
    
  if (OTHER_LOGIC STATEMENT){
    //Do this line
    //and this line
    k++; //increase the value of k by 1
  }
}

Our full loop will llok like this.

var r = new Random();
for (int i = 0; i < total_iterations; i++){
  double x = r.NextDouble();
  double y = r.NextDouble();
  if (Sqrt(Pow(x,2) + Pow(y,2)) < 1)
    count_inside_quarter_circle++;
}

And finally, print out the answer. Note we are casting to a double. Otherwise, the arithmetic will return an integer value.

Console.WriteLine((double)4 * count_inside_quarter_circle / total_iterations);

You can test this online at https://repl.it/ or http://rextester.com/.

The full file should look like this. C, C++, C#, will all have very similar implementations as what is shown in the following file.

Calculating with Ocaml

Ocaml is a functional programming language so it is quite different than the last two examples. There are no type declarations like in C# but the type is inferred based on context. Arithmetic operators must be specifically chosen for the type being used.

Basic function:

let f x = float_of_int x in

The name of this function is f and takes in one parameter x. The return of this function is the return of the function float_of_int x. Basically, you can think of this function as an alias. We don’t want to write float_of_int x everywhere. Instead, we would rather write f x. The in keyword is defining function f in the all of the code leading up to a ;;.

let hyp a b = sqrt((a *. a ) +. (b *. b)) in

This function called hyp takes in two parameters a and b. You will notice that the expression on the right-hand side has *. and +. operators. These are operators used on floating point numbers. By using these the ocaml compiler knows that a and b must be floats and will issue an error if we try to pass in an integer.

let randcheck () = hyp (Random.float 1.0) (Random.float 1.0) < 1.0 in

The randcheck function takes in an empty parameter. This makes sure that each time the function is called it will be reevaluated. This functions passes 2 random floats to the hypotenuse function and returns a logical true and false depending on if the hypotenuse is less than or greater than 1. Note that the Random.float function takes a float value as an argument. This argument limits the maximum return value and also note that it is 1.0 (a float) and not 1 (an int).

let total_iterations = 1000000 in

This function is only evaluated once since no arguments are passed into it.

let count_inside_quarter_circle = ref 0 in

This function defines a reference to a variable. This way we can change the value of the variable. By default, it is set to 0.

Finally lets deal with the for loop.

for i = 1 to total_iterations do
  let a = if  (randcheck ()) then 1 else 0 in
  count_inside_quarter_circle := !count_inside_quarter_circle + a;
done;

the ! and := operators are how we derefence the value inside count_inside_quarter_circle and how we then put a new value in.

Finally let’s print.

print_string (string_of_float ( 4.0 *. ( (f !count_inside_quarter_circle) /. (f total_iterations) )));;

You can try this online at tutorialspoint.

The full file should look like this.

Making it your Own

Your turn to make some changes. We have set the number of iterations as an endpoint for each loop. Instead try modifying the code to stop looping once a minimum accuracy has been reached.

That’s All Folks